Algebra Simplify (3n)^2 (3n)2 ( 3 n) 2 Apply the product rule to 3n 3 n 32n2 3 2 n 2 Raise 3 3 to the power of 2 2 9n2 9 n 21 Show that (n^3 3n^2 3n 1) / (n 1) is O(n^2) Use the definition and proof of bigO notation 2 Prove using the definition of Omega notation that either (8^n) is (omega) (5^n) or not Question 1 Show that (n^3 3n^2 3n 1) / (n 1) is O(n^2) Use the definition and proof of bigO notation 2M3n3m(m2n2)n(mn)2 Final result m • (2m 3n) • (m n) Step by step solution Step 1 Equation at the end of step 1 (((m3)(n3))(m•((m2)(n2))))n

Principle Of Mathematical Induction Class Xi Exercise 4 1 Part 2 Breath Math
Prove that (n-1)^2+n^2+(n+1)^2=3n^2+2
Prove that (n-1)^2+n^2+(n+1)^2=3n^2+2-Write an inequality that describes the situation Place the correct answer in the blank 1) Determine the limit by substitution lim x2 3x 4 A 6 B 2 C 2 D undefined Find the slope of the line passing through the given points (5, 14) and (1, 2) A) 3 B 3 D 4 E 9I don't get how the answer is #1/12#




Prove The Following 1 4 7 3n 2 N 3n 1 2 Homeworklib
We have proved the contrapositive, so the original statement is true Note that if n is of the form 2^k, then n's prime factorization is only composed of 2's Thus, the contrapositive of the original statement is as follows n = b* (2^k), where b is a positive odd number ==> 2^n 1 is composite Let n = b* (2^k)If Number N 2, 4n 1 and 5n 2 Are in AP Find the Value of N and Its Next Two TermsWhat is N Redundancy?
First off (n^2 n 1)/ (3n^2 1) = 1 ( 2n^2 n 2/ 3n^2 1 ) = 1 r (subn) The question tells me to show that r (subn) approaches 2/3 Hence we need to find the remainder r (subn) I tried finding the remainder by doing this Find an expression which is greater than (2n^2 n 1)In a G P the ratio of the sum of the first eleven terms to the sum of last eleven terms is 8 1 and the ratio of the sum of all terms without the first nine to the sum of all the terms without the last nine is 2Then the number of terms of the G P isThe equation is now solved n^ {2}3n1=y^ {2} Swap sides so that all variable terms are on the left hand side n^ {2}3n=y^ {2}1 Subtract 1 from both sides n^ {2}3n\left (\frac {3} {2}\right)^ {2}=y^ {2}1\left (\frac {3} {2}\right)^ {2} Divide 3, the coefficient of the x term, by 2 to get \frac {3} {2}
Why create a profile on Shaalaacom?If the sum of the first ten terms of the series ( 1 3 5) 2 ( 2 2 5) 2 ( 3 1 5) 2 4 2 ( 4 4 5) 2 , is 16 5 m, then m is equal to 7 Let p = lim x → 0 ( 1 tan 2 8 For x ϵ R, f ( x) = log 9 For x ∈ R, x ≠ 0, x ≠ 1, let f 0 ( x) = 1 1 − x and f n 1 ( x) = f 0 ( f n ( x)), n = 0, 1, 2, O(2^(n1)) is the same as O(2 * 2^n), and you can always pull out constant factors, so it is the same as O(2^n) However, constant factors are the only thing you can pull out 2^(2n) can be expressed as (2^n)(2^n), and 2^n isn't a constant So,




2 5 8 3n 1 3n 2 N 2 Free Math Help Forum




Ex 4 1 16 Prove 1 1 4 1 4 7 1 3n 2 3n 1 N 3n 1
which expression represent the product of 2 consecutive odd integers where n is an odd integer? n^23n2 We can rewrite the numerator as ((n2) * (n21) * (n22)!)/((n)!) =((n2) * (n1) * (n)!)/((n)!) We can cancel (n)! You have done everything absolutely correctly, but was not able to find a sum You got n n/2 n/4 , which is equal to n * (1 1/2 1/4 ) You got a sum of geometric series, which is equal to 2Therefore your sum is 2nSo the complexity is O(n) PS this is not called telescoping Telescoping in math is when the subsequent terms cancel each other




Write The First Three Terms Of Sigma Infinity Chegg Com




What Is The Simplified Form Of 3 N 2 3 N 3 3 N 1 Quora
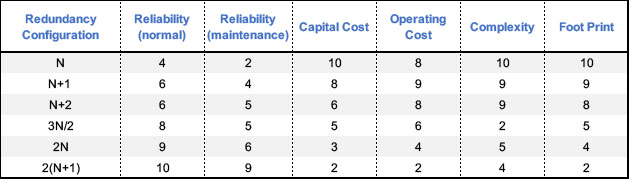
N, N1, N2, 2N, 2N1, 2N2, 3N/2 Redundancy can be broken down into several different levels A quick recap of redundancy levels includes key terminology such as N, N1, N2, 2N, 2N1, 2N2, 3N Get an answer for '`1 4 7 10 (3n 2) = n/2 (3n 1)` Use mathematical induction to prove the formula for every positive integer n' 2^3n – 1 is divisible by 7, for all natural numbers n asked in Mathematics by AsutoshSahni ( 526k points) principle of mathematical induction



Q Tbn And9gcrec Fpj 2t8s94cnm4cc5btkwpw14s3lijl56cedgictrqw Qk Usqp Cau



Http Www Geometer Org Mathcircles Indprobs Pdf
数列求和 求数列 10(3n1) / (3n1)(3n1)(3n2) 从1加到n项的和 1年前 2个回答 如果对于不小于8的自然数n,当3n1是一个完全平方数是,n1都能表示成个k完全平方数的和,那么k等于多少?N is simply the amount required for operation It represents the capacity that you need to operate1 Inform you about time table of exam 2 Inform you about new question papers 3 New video tutorials information



Lim N Gtoo N 1 N 2 3n N 2n 1 N Is Equal To Youtube




Ncert Solutions For Class 9 10 11 And 12 Prove The Following By Using The Principle Of Mathematical Induction For All N N
Solution for 5n^2n3=3n^23 equation 5n^2n3=3n^23 We move all terms to the left 5n^2n3(3n^23)=0 We add all the numbers together, and all the variables 5n^21n(3n^23)3=0 We get rid of parentheses 5n^23n^21n33=0 We add all the numbers together, and all the variables 2n^21n=0 a = 2; Ex 41, 5 Prove the following by using the principle of mathematical induction for all n N 13 232 333 n3n = ((2 1) 3^( 1) 3 )/4 Let P(n) 13 2Step 1 Equation at the end of step 1 (((n 3) 3n 2) 3n) 1 Step 2 Checking for a perfect cube 21 n 33n 2 3n1 is not a perfect cube Trying to factor by pulling out 22 Factoring n 33n 2 3n1 Thoughtfully split the expression at hand into groups, each group having two terms




Principle Of Mathematical Induction Class Xi Exercise 4 1 Part 2 Breath Math




Serieshw 2
Click here👆to get an answer to your question ️ Let P (n) = 2^3n 7n 1 then P(n) is divisible by Join / Login > 11th > Maths > Principle of Mathematical Induction >Bn1 です。 これらを a n 2 = 8( n 2) a n 1 7( n 2 3 n 2) a n に代入すると解くことができますよ。 まあ、少し解答がエレガンスでないですが、確実に解けるのでこちら側の解法でもいい1 ab 2 a*b 3 ab 4 a/b Calculus, check my answer, please!



Prove That The Sum From 1 To Of 2n 3n 6n 3 2 Stumbling Robot




Solved 5 Prove Mathematical Induction N Z0 12 32 52 2n 1 2 N 1 2n 1 2n 3 1 3 Prove N Integer 3n 2 Q
N, N1, N2, 2N, 2N1, 2N2, 3N/2 Redundancy can be broken down into several different levels A quick recap of redundancy levels includes key terminology such as N, N1, N2, 2N, 2N1, 2N2, 3N/2 What do these terms mean?2 (b) Which term of the sequence with general term 3n−1 5n7 is 7 12 ?Δ = b 24ac Δ = 1 24·2·0 Δ = 1 The delta value is higher than




A Binary Matrix Of Size N 2 N 1 1 3n 2 2n For Forming A Download Scientific Diagram



Sum Of N Terms Of Series
Advanced Math Advanced Math questions and answers (a) Is an = 3n2 n−4 a general term of a sequence? These configurations take various forms, such as N, N1, N2, 2N, 2N1, 2N2, 3N/2, among others These multiple levels of redundancy topologies are described as NModular Redundancy (NMR) N refers to the bare minimum number of independent components required to successfully perform the intended operationTìm n thuộc Z 1)n5 chia hết n 2)3n2 chia hết n 3)2n3 chia hết n 4)5n chia hết n1 5)4n chia hết 1n 6)103n chia hết 1n 7)n5 chia hết 1n 8)3n5 chia hết n1 9) 2n3 chia hết 2n1 10) 6n5 chia hết 3n2




Follow Me For A Walk Through Mathematical Induction




Calculus Find The Radius Of Convergence For 3n Online Presentation
In Exercises 115 use mathematical induction to establish the formula for n 1 1 12 22 32 n2 = n(n 1)(2n 1) 6 Proof For n = 1, the statement reduces to 12 = 1 2 3 6 and is obviously true n(3n 1) 2 Proof For n = 1, the statement reduces to 1 = 1 2 2 and is obviously true Assuming the statement is true for n = k 1 4 7 lim(n →∞)((n 1)(n 2)3n)/n2n)1/n is equal to (A) 3log3 2 (B) 18/e4 27/e2 (D) 9/e2 Welcome to Sarthaks eConnect A unique platform where students can interact with teachers/experts/students to get solutions to their queriesB = 3 and f(n) = n^2 f(n) = n/2 f(n) 1, this means that f(n) = O(n) Also f(n) >= 08*(n/2) for all n > 1, this means that f(n) = omega(n) Hence f(n) = θ(n) Therefore, the solution is T(n) = θ(nlogn) Share Cite Improve this answer Follow answered Sep 4




Can You Help Me To Solve Recurrence Relation T 1 5 And For All N 2 T N 2t N 1 3 N 1 Stack Overflow
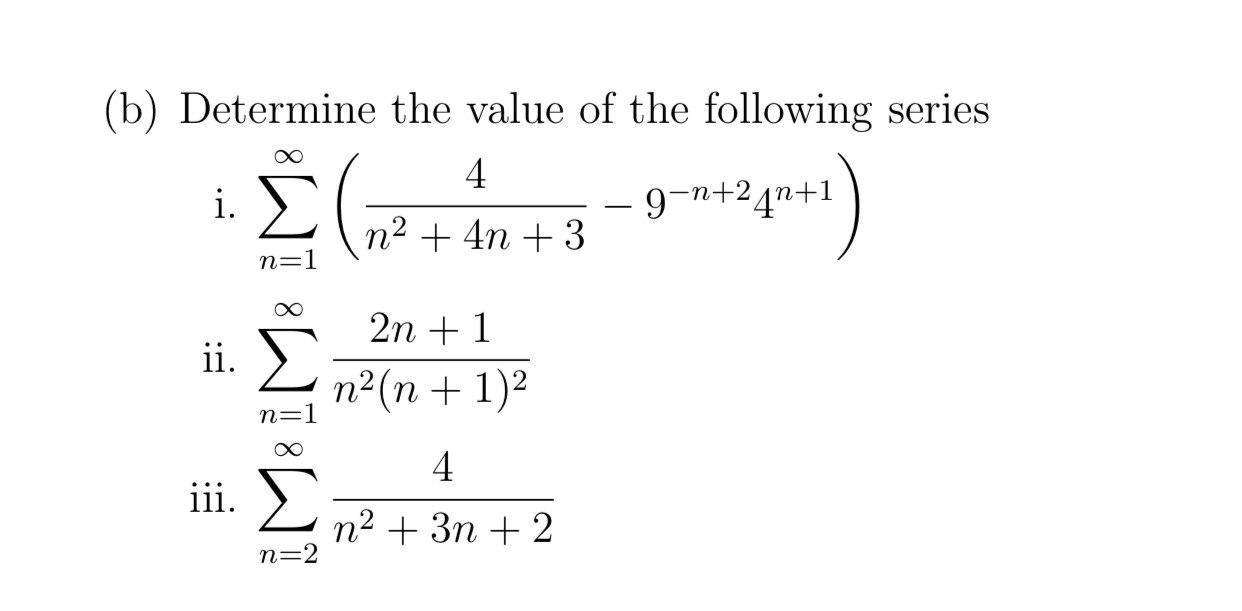



Answered B Determine The Value Of The Bartleby
#sum_(n=1)^oo 1/((3n2)(3n1))# There is an infinity sign on the top of the summation sign and n=1 on the bottom Please write in details;4 Calcular el l mite de la sucesi on de t ermino general a n= p n2 n 1 p 3n2 1 3n Soluci on Debido a la indeterminaci on 11 , procedemos as L = l m n!1 (p n2 n 1 p 3n2 1) l m n!1 Given that, ( 9^n x 3^2 x (3^n/2)^2 27^n) /( 3^3m x 2^3) = 1/27⇒ (3^2n x 3^2 x { 3^(2n/2) } 3^3n )/ 3^3m x 2^3 = 1/(3^3)⇒ (3^2n x 3^2 x {3^n} 3^3n )/




1 Simplify 3 N 2 3 N 1 4 3n 3n Brainly In



Http Www D Umn Edu Jgreene Honors calculus Exam 3 11 Sol Pdf
Transcript Prove 1 2 3 n = (n(n1))/2 for n, n is a natural number Step 1 Let P(n) (the given statement)\ Let P(n) 1 2 3 n = (n(n1))/2 StepFind stepbystep Discrete math solutions and your answer to the following textbook question Find gcd(2n 1, 3n 2), where n is a positive integer3n2 = 3 (2k) 2 = 6k 2 The term 6k is always even and 2 is odd Accordingly, 6k 2 is even Thus, 3n 2 is even This implies that the statement "if n is even then 3n2 is even" is true Therefore, the contrapositive "If 3n2 is odd, then n is odd" is also true Hence proved




For All N Inn 3 5 2n 1 2 3n 1 Is Divisible By A 19 B 17




2bm2 Show By Mathematical Induction That 1 4 7 3n 2 3n 2 N Over 2 Youtube
Simple and best practice solution for 2(n1)4n=2(3n1) equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand, so don`t hesitate to use it as a solution of your homework If it's not what You are looking for type in the equation solver your own equation and let us solve it $$\left(1 \frac1{3n}\right)^{1/n} \to 1^0=1$$ we reduce to evaluate the limit for $(3n^2)^\frac1n=3^\frac1n \,\left(n^\frac1n\right)^2$ As an alternative we can use thatSolve for n 21/2n=3n16 2 − 1 2 n = 3n 16 2 1 2 n = 3 n 16 Combine n n and 1 2 1 2 2− n 2 = 3n 16 2 n 2 = 3 n 16 Move all terms containing n n to the left side of the equation Tap for more steps Subtract 3 n 3 n from both sides of the equation 2 − n 2 − 3 n = 16 2 n 2 3 n = 16




A Binary Matrix Of Size N 2 3n 2 To Form The Set Of Diagonal Download Scientific Diagram



1 1 4 1 4 7 1 7 10 1 3n 2 3n 1 N 3n 1 Sarthaks Econnect Largest Online Education Community
2 (c) An arithmetic sequence has its 4 th term equal to 18Giá trị của A = lim 2n23n1 3n2−n2 A = l i m 2 n 2 3 n 1 3 n 2 n 2 bằng Câu hỏi trong đề 75 câu trắc nghiệm Giới hạn cơ bản !!You know the limit (it is indeed log(4/3)), but you probably want to know why it is what it is The easiest way is probably to compare the sum to the integral ∫dx/x from 3 to 4, which is of course log(4/3) Cut up the interval 3, 4 into n subint



If 3 N 4 3 N 2 8 What Is The Value Of N Quora




Find The Sum Of The Series Sum N 1 Infty Frac 3n 2 N Mathematics Stack Exchange
Out =((n2) * (n1) * 1)/11)n(n1) 2)n(n2) 3)n(n3) 4)2n1 help me plz if a and b are both odd integers, which expression must always equal an odd integer?Question 3n^2 n/n^2 1 n^2/n 1Multiply or DividePlease show your work Related Answer More Related Question & AnswersMore Related Question & Answers



What Is Math Sum N 0 Infty Left Frac 1 3n 1 Frac 1 3n 2 Right Math Quora




Answered Prove The Following N 3p 1 For Every Bartleby
Step 1 Step 2 Pulling out like terms 21 Pull out like factors 2n 1 = 1 • (2n 1) Equation at the end of step 2 3n 2 • (2n 1) Step 3 Step 4 Pulling out like terms 41 Pull out like factors n 2 = 1 • (n 2) Final result n 2If the numbers (2n1), (3n2) and (6n1) are in AP, find n and hence find these numbersNumber n is the product of n factors, starting with n, then 1 less than n, then 2 less than n, and continuing on with each factor 1 less than the preceding one until you reach 1




Prove 1 4 7 3 N 2 N 2 3 N 1 By Mathematical Induction For All N Belongs To N Maths Principle Of Mathematical Induction Meritnation Com




1 N 1 In N N 1 S N N 1 N
To ask Unlimited Maths doubts download Doubtnut from https//googl/9WZjCW `1222^232^3n2^n=(n1)2^(n1)2`




Review Evaluate The Expression For The Given Value Of N 3n 2 N 4 N 2 3n N 6 10 And Ppt Download




Use The Ratio Test To Determine Whether The Series Is Chegg Com




3 6 9 3n 3n N 1 2 Brainly In



Www Mtholyoke Edu Courses Jmorrow Calculus Ii Factexsolns Pdf




Answered I Proving A Formula Use Mathematical Bartleby
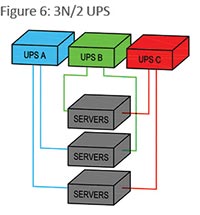



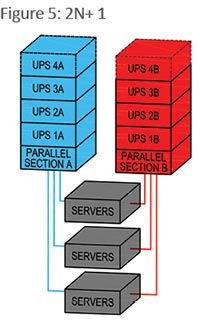
2 N 1 And 3n 2 Redundancy High Reliability Options Facilities Management Insights




Prove The Following 1 4 7 3n 2 N 3n 1 2 Homeworklib




The N Th Term Of The Sequence Is 3n 2 Is The Sequence An Ap If So Find The 10th Term Youtube



What Is The Sum Of N N 1 N 2 2n Quora



2



1



What Is Lim 3 N 2 N 1 2n When N Tends To Infinity Quora



Link Springer Com Content Pdf 10 1007 2f978 3 7091 6146 3 12 Pdf




1 4 7 3n 2 N 3n 1 2 Brainly In



Data Center Redundancy N 1 2n 2 N 1 Or 3n2 Distributed



2 N 1 And 3n 2 Redundancy High Reliability Options Facilities Management Insights



1




Ex 4 1 16 Prove 1 1 4 1 4 7 1 3n 2 3n 1 N 3n 1



1 4 7 10 3n 2 N 3n 1 2 Sarthaks Econnect Largest Online Education Community




User Dcljr Series Wikibooks Open Books For An Open World




An Introduction To Mathematical Induction The Sum Of The First N Natural Numbers Squares And Cubes Math Wiki




Prove That 1 3n 2 1 3n 1 1 3n 1 3n For N Chegg Com




Ex 4 1 16 Prove 1 1 4 1 4 7 1 3n 2 3n 1 N 3n 1
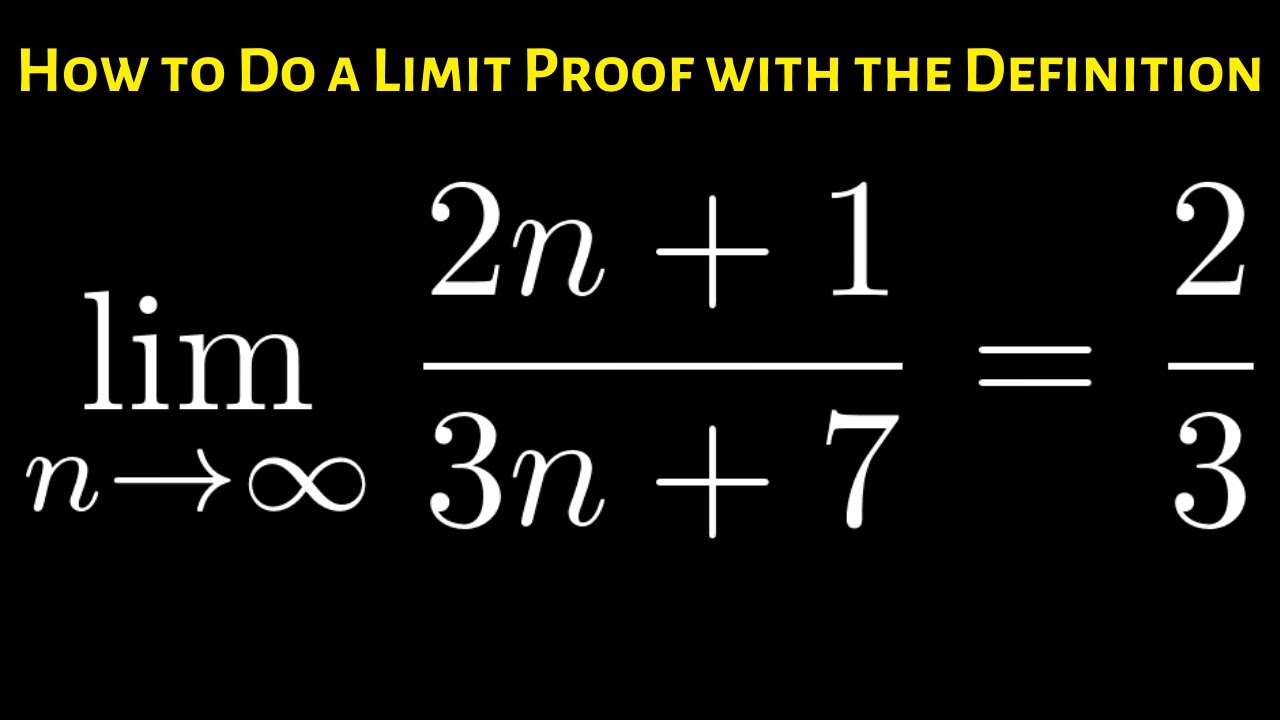



How To Prove That The Limit Of 2n 1 3n 7 As N Approaches Infinity Is 2 3 Youtube




Ex 4 1 16 Prove 1 1 4 1 4 7 1 3n 2 3n 1 N 3n 1




1 Point Select The First Correct Reason On The List Why The Given Series Converges D 1 34 Homeworklib




P N 1 4 7 3n 2 1 2n 3n 1 P T By Principle Of Mathematical Induction Brainly In



Www3 Nd Edu Dgalvin1 S08 Exam3 Solns Pdf




Use The Ratio Test To Determine The Convergence Or Divergence Of The Series S N 1 1 N 2 4 6 2n 2 5 8 3n 1 Homework Help And Answers Slader




For An 1 Why Is It Equal To 2n 1 2n 1 Chegg Com




Prove Using Mathematical Induction That 2 3n 3 N Is Divisible By 5 For All N 1 Mathematics Stack Exchange
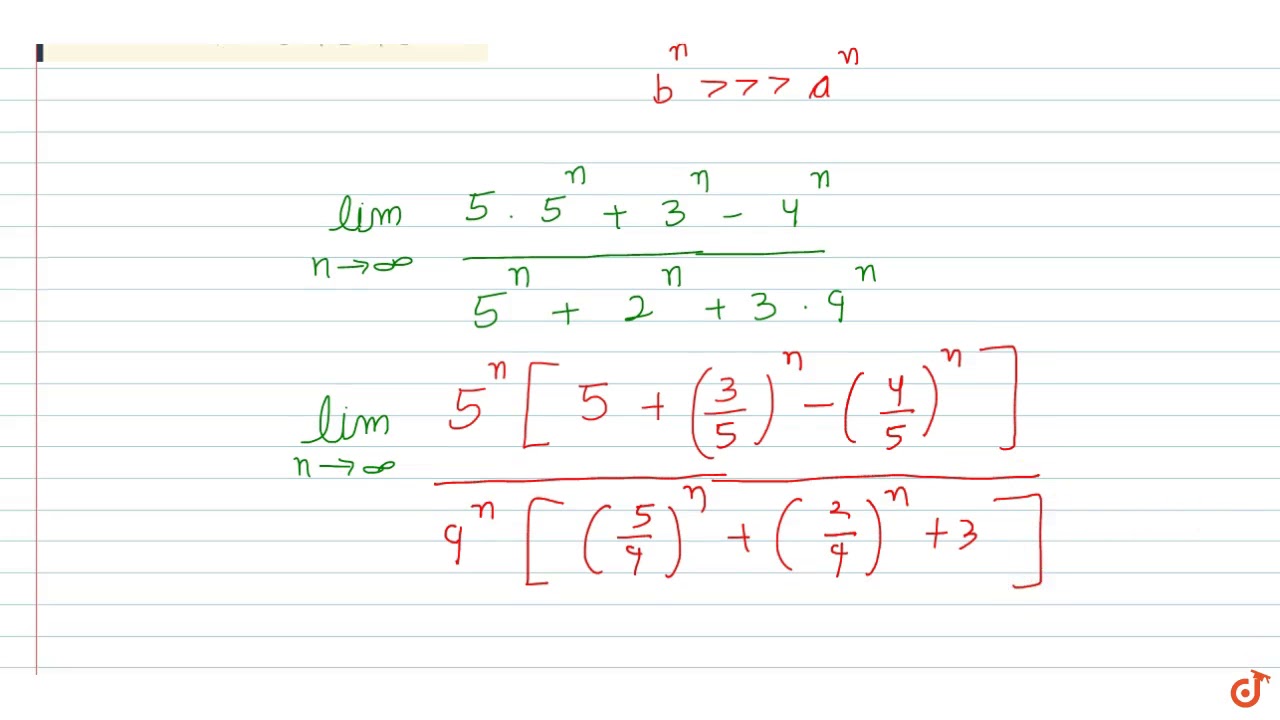



Lim N Gtoo 5 N 1 3 N 2 2n 5 N 2 N 3 2n 3 Youtube




N N 1 N 2 2n 2n 1 2n 2 3n 2 Redundancy Explained Bmc Software Blogs



If The Numbers 2n 1 3n 2 And 6n 1 Are In Ap Find The Value Of N And The Numbers Sarthaks Econnect Largest Online Education Community




If F N N 1 2 3n Which Statement Is True 1 F 3 2 2 F 2 3 3 F 2 15 4 F 15 Brainly Com




Prove The Following By Using The Principle Of Mathematical Induction For All N N 1 2 5 1 5 8 1 8 11 1 3n 1 3n 2 N 6n 4 Mathematics Shaalaa Com



Find The Sum Of The Series 2n2 3n 5 To N Terms Mathematics Topperlearning Com Gdsw8eo66
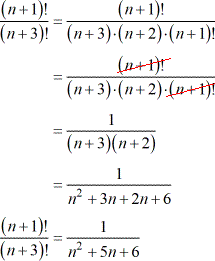



Simplifying Factorials With Variables Chilimath



Www Colorado Edu Amath Sites Default Files Attached Files Archive Appm1360fall18exam3 Sol Pdf




Mathematical Induction Rosen 3 3 Basics The Wellordering




Sum Of N N Or N Brilliant Math Science Wiki




Show That 1x2 2 2 X 3 2 N N 1 2 1 2 X 2 2 2x3 N 2 N 1 Maths Meritnation Com




Chapter 3 Cbu



Link Springer Com Content Pdf 10 1007 2f978 3 7091 6146 3 12 Pdf




Use Mathematical Induction To Prove One Of The Chegg Com




Lim N Oo 1 N 2 N 1 3 N 2 N 1 1 2 2 2 3 2 N 2



1




Ex 4 1 10 Prove 1 2 5 1 5 8 1 8 11 1 3n 1 3n 2



2




1 N2 N 1 N2 N N 3 N2 3n 2 Shkolnye Znaniya Com




7cgy2oifhyvqxm




Problems To Solve Involving Induction Proof By Induction Basis Step Does It Work For N 0 Ppt Download




If The Sum Of N Terms Of An Ap Is 3n 2 2n Find Its R Th Term Mathematics Topperlearning Com 9em1b0aa



Simplify I n 3 A 2n 1 N 2 A3 2n 1 An 2n 1 Studyrankersonline



If Math S N 3n 2 2n Math Is The Sum Of First Math N Math Terms Of Arithmetic Progression How Do You Find The Second Term Of The Sequence Quora




Prove By Induction 1 2 2 2 N 2 2n 3 Chegg Com




Demostracion Por Induccion 1 4 7 3n 2 Youtube



M 2 N 1 N 2 Figure 3 M 2 N 1 3n 2 Download Scientific Diagram




N 3n 1 A For Each Natural Number 1 4 7 3n Chegg Com




Prove The Following By Using The Principle Of Mathematical Induction For All N N 1 1 4 1 4 7 1 7 10 1 3n 2 3n 1 N 3n 1 Mathematics Shaalaa Com




6 8 N 1 16 2 3n 2 10 2 3n 1 7 8 N




Assignment 4 Sum Of Arithmetic Series




Using Mathematical Induction To Prove 2 3n 3 N Is Divisible By 5 Youtube




Evaluate Lim N 1 N 1 N 1 1 N 2 1 3n Youtube




Ncert Solutions For Class 9 10 11 And 12 Prove The Following By Using The Principle Of Mathematical Induction For All N N




Ex 4 1 5 Prove 1 3 2 32 3 33 N 3n 2n 1 3n 1




Prove That 2n 1 2n 3 Dots 4n 1 3n 2 By Induction Mathematics Stack Exchange




Calculus Find The Radius Of Convergence For 3n Online Presentation




Rd Sharma Solutions For Class 11 Maths Updated 21 22 Chapter 12 Mathematical Induction Download Free Pdf




Determining The Big O Runtimes Of These Different Loops Stack Overflow



Limit Limit N N 1 N 2 3n N 2n 1 N Is Equal To Sarthaks Econnect Largest Online Education Community




Find The Sum Of The Series Whose Nth Term Is Given By 3n2 3n 2 Maths Sequences And Series Meritnation Com




If The Numbers 2n 1 3n 2 And 6n 1 Are In Ap Find N And Hence Find These Numbers Youtube




Pg 601 Homework Pg 606 1 6 8 11 16 2n 2 3n 1 5 7 3n 2 7n 2 84n N 2 21 23 26 29 33the Series Ppt Download



0 件のコメント:
コメントを投稿